Technical basics series: PCA for "A/B" testing

Here’s an outline for using PCA for ranking feature importance and doing an “A/B” test. See here for an introduction to PCA via matrix factorizations.

PCA gives us a way to reorganize a matrix (or in this case, a data set of examples as rows and features as columns) as a sum of approximations such that

• The approximations are ordered by how much they contribute to the data set
• The reorganized columns are actually combinations of the original features in the data set

Usually, we assume that the approximations that have the largest contributions are also the most important. So PCA will not only create a smaller number of derived features (potentially helping with overfitting) but those derived features can reveal feature importance.†

Problem statement

So let’s say you have some labeled data that has two categories, the A-set and the B-set.

1. Can I learn critical features, which I’m defining as both important and distinguishing between the A and B sets?
2. Are there subsets of the features that are most important for doing prediction. (In this case, I would not separate the data into A and B sets.)

Answering number 2 first: if you choose enough components for PCA, you should be able to explain enough of the variance in the data set. For example, with the Encore data set I’ve been looking at, only 30 columns are required to explain over 90% of the variance. You can then feed this approximation to your classifier of choice for good accuracy too; I got > 90% wit a gradient boosted tree.

Now for number 1. Here’s what PCA gets us. The image below shows four “color columns” / features of data.

That’s 4 columns. Way too many. With PCA, we can choose an approximation with, say, 2 columns:

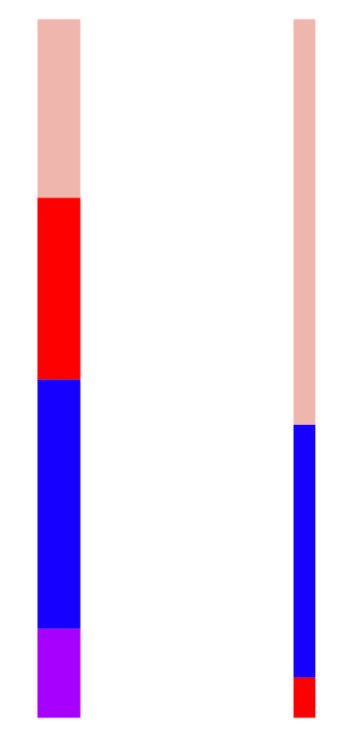
The left column is “wider” because it is the first component of PCA, and the first component is the most important. We can see the blue feature makes up the largest part of the first component. The other column is the second component of PCA. It is not as important as the first (meaning it contributes less to the original matrix / data set), but within it, the beige feature is the most important part.

To try to get a sense of feature distinction between A and B, I did the following:

1. Chose the number of components for PCA (20, in my test case)
2. Perform a PCA on both the A- and B-set, get back a list of features that contribute the most to each component. For example in the above example, it would return: [ (0, blue), (1, beige) ].
3. I have this list for both the A and B category. Now, for each feature in the A-set, I look at the histogram of that feature in both the A- and B-set. Here are a few examples:

So now I have two histograms. Do I have look at every feature paired up this way? Well, no. Besides looking at them, there are at least three ways of judging how similar two histograms are:

• Kolmogorov-Smirnov test, which reports a statistic (the higher, the more likely the two histograms are from the same underlying distribution) and the p-value (the lower it is, the more unlikely it is that two histograms would be this different from just random noise).
• Bayesian modeling: we specify a generative model for the counts that we see. For example, count data as in a histogram is usually Poisson-distributed, so we could have a simple model: lambda_1 ~ Gaussian(mu, sigma), lambda_2 ~ Gaussian(mu, sigma), histogram_1 ~ Poisson(lambda_1), histogram_2 ~ Poisson(lambda_2)
• Good ol' cosine similarity on the vectors of the bin values in the histograms.

However we define the similarity, once we have it, we can set a threshold over which we can declare the histograms different.

Once we have a feature that is both important (from a low PCA component number) as well as distinguishing (histogram similarity is low), it should be worth having a client or BIA examine it.

Notes

†Whenever you see DataRobot mention that PCA is used as part of its pipeline, it’s most likely doing both dimensionality reduction as well as contributing to feature importance.